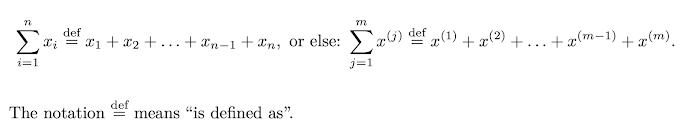Machine Learning - Notation and Definitions - Part 2

Notation and Definitions

1) Capital Sigma Notation: 

The summation over a collection X = {𝒙₁, 𝒙₂,...,𝒙_n-1, 𝒙_n} or over the attributes of a vector x = [𝒙⁽¹⁾, 𝒙⁽²⁾,...,𝒙^(m-1), 𝒙^(m) ] is denoted like this:

2) Capital Pi Notation:

It denotes a product of elements in a collection or attributes of a vector:

3) Cardinality of Set:

The cardinality of a set is a measure of a set's size, meaning the number of elements in the set. It is denoted as |A|.

For instance, the set A = { 1 , 2 , 4 } then |A| = 3 since there are only three elements in set A such as 1,2 and 4.

Referenced The Hundred-Page Machine Learning Book - Andriy Burkov

Machine Learning - Notation and Definitions - Part 1

 Notation and Definitions

  1) Scalars, Vectors, and Sets:

   A scalar is a simple numerical value, like 15 or - 3.25. 

   Variables or constants that take scalar values are denoted by an italic letter, like 𝒙.

   A vector is an ordered list of scalar values, called attributes. We denote a vector as a bold character, for example, x or w.

   A set is an unordered collection of unique elements. 

a 

   If a set includes all values between a and b, including a and b, it is denoted using brackets as [a, b].

   For example, the set [0, 1] includes such values as 0, 0.0001, 0.25, 0.784, 0.9995, and 1.0.

   If the set doesn’t include the values a and b, such a set is denoted using parentheses like this: (a, b). 

   For example, the set (0, 1) includes such values as 0.0001, 0.25, 0.784 and 0.9995 but doesn't include 

   0 and 1.

   A special set denoted ℝ includes all numbers from -∞ (minus infinity) to +∞ (plus infinity).

   When an element 𝒙 belongs to a set S, we write 𝒙 ∈ S.

   We can obtain a new set S₃ as an intersection of two sets S₁ and S₂. In this case, 

   we write S₃ ← S₁ ∩ S₂.

   For example {1, 3, 5, 8} ∩ {1, 8, 4} gives the new set {1, 8}. 

   We can obtain a new set S₃ as a union of two sets S₁ and S₂. In this case, we write S₃ ← S₁ ∪ S₂. 

   For example {1, 3, 5, 8} ∪ {1, 8, 4} gives the new set {1, 3, 4, 5, 8}.

Referenced The Hundred-Page Machine Learning Book - Andriy Burkov